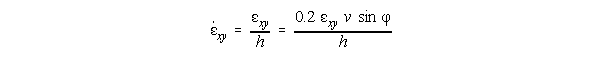
The analysis of the strain rate in metal cutting is one of the most
important yet not fully understood problems. The question concerning the
order of strain rate in metal cutting is one of the oldest problems and
has existed throughout the modern history of metal cutting. Because this
problem is of great interest for both theory and practice, the next section
addresses this topic.
1 Reported strain rates
The high strain rates which are believed to occur in metal cutting may affect the mechanical properties of workpiece material significantly by modifying the relevant mechanical properties of workpiece material. Moreover, if the strain rate encountered in metal cutting process is high and can be adequately determined, then metal cutting may become a very important testing method for the determination of the dynamic physical properties of machinable materials. Such a possibility was suggested by Drucker [1] and Shaw [2].
Drucker [1] assumed that the mean rate of shear strain exy
is equal to the mean shear strain exy
divided by the average time tav required to traverse
the parallel-sided shear zone of thickness h t1 /20 (t1
is the uncut chip thickness):
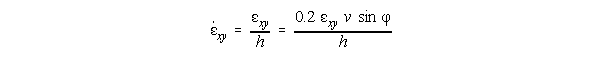
Assuming exy = 2, h = 0.010 in, v = 200 fpm, and = 15 deg, Drucker calculated a e' xy = 40,000 sec-1 and stated that only for very low cutting speeds, v, and large uncut chip thicknesses, t1, the values of xy in metal cutting approach those obtained in high-speed impact experiments.
Freudenthal [3] assumed v = 100 fpm, t1 = 0.01
in, = 20 deg, a thickness of glide lamellae h1
in the order of magnitude of 4 × 10-5 in, and
a exy in the order of magnitude
of 0.1. He then calculated the strain rate as:
Freudenthal stated that the strain rate, obtained in this way, exceeds that imposed by impact loads applied at bullet velocities.
Chao and Bisacre [4] stated that the strain rate commonly found in machining operations is estimated to be of order of 103 to 106 sec-1.
Shaw [2] derived the following relationship for strain
where Dy is the spacing between successive shear planes. Assuming a reasonable cutting regime, Shaw calculated a mean shear strain rate of 213,000 sec-1. Shaw stated that the maximum of this rate might be many times this value and may reach the order of 106 sec-1 which is very high compared to the strain rate in an ordinary tensile test of about 10-3 sec-1 and 103 sec-1 in the most rapid impact tests.
Kececioglu [5] attempted to determine the strain rate in metal cutting experimentally. Studying different workpiece materials and using variety of cutting regimes, he obtained a range for the mean shear strain rate from 2,500 to 212,000 sec-1. Based on this result, Kececioglu concluded that under metal cutting conditions dislocations may be moving with the velocity of sound or faster.
Von Turkovich [6] concluded that the strain rate under common metal cutting conditions is of 2 × 104 c-1, and at very high cutting speeds and very shallow feeds, the strain rate can be very large, on the order of 107 c-1.
Oxley studied the strain rate and its effect in metal cutting for many years [7-9] and concluded that the average shear strain rate in the shear zone lies in a range from 103 to 105 c-1 or even higher. Most of studies, published in recent years (see, for example, References 10 and 11) consider the same range for the rate of strain following his approach.
The analysis above shows that there is a high consistency in the reported
results. Any objection to the discussed results could not be located in
the literature available to the author.
2 Critical analysis of the reported strain rates
From the foregoing, it is seen that, as believed, the strain rate in metal cutting is higher than that in most rapid impact tests and even exceeds that imposed by impact loads applied at bullet velocities. In the author's opinion, the strain rate in cutting is considered to be extremely high because it is thought of in terms of the known velocity diagrams and the assumed model of a deformation zone with zero-thickness. In this case, any strain rate, even an infinite, can be obtained. To understand this point, however, there is not need to consider even the speed of a bullet. As is well known, the working speeds encountered in different metal-forming operations is much higher than that in cutting ( see Table 15.1 in Dieter [12] ). It can be found on the very same page that the drawing of a fine wire at speed 120 ft/s (that is much higher than the cutting speed, and the deformation zone is very small) can result in a strain rate in exceed of 105 s-1. It is also shown in Dieter [12] that some modern metalworking processes utilize velocities as high as 700 ft/s to carry out forging, extrusion, sheet forming, etc. These processes are known as high-energy-rate forming. These high-velocity processes utilize the energy from explosion (gas or conventional explosive); however, the calculated strain rate in metal cutting is still higher than those in these processes. Moreover, contradictory to the common sense, the strain rate in cutting is even higher than that of a bullet hitting a wall [13]. In our opinion, the sense of order of the strain rate has been missing in metal cutting studies. We feel that a greater understanding of the mechanical properties of materials in metal cutting is necessary; therefore, the question about the real value of the strain rate in metal cutting has to be clarified.
Classification of various types of loading in terms of the strain rate is presented in Figure 3.19 [14]. Upon examining the present state of research within the individual areas indicated in this figure, it is found that for strain rates of less that 10 s-1, reliable, commercially available experimental apparatus and standard methods for the evaluation of results already exist. A rather different situation exists at strain-rates, which are greater than about 104 s-1. As can be seen from Figure 3.19, the role of material internal forces cannot be neglected in this region. Nevertheless, Oxley [9] and many others researchers neglected this forces while reporting high strain rates. Moreover, when the rate of strain falls in this region, a description of the corresponding force effects must include the propagation of the stress waves and/or stress pulse [14]. This approach has never been considered in metal cutting studies.
Additional support to the author's argument is the aspect of metal plastic deformation. There are two principle different mechanisms of plastic deformation of metals: plastic deformation by slip and by twinning [12, 15].
The usual method of plastic deformation in metals is by the sliding of blocks of the crystal over one another along definite crystallographic planes, called slip planes. Slip occurs when the shear stress exceeds a critical value. The atoms move an integral number of atomic distances along the slip plane and the step is produced in the polished surface. When the polished surface is viewed from above with a microscope, the step shows up as a line called a slip line.
The second important mechanism by which metals deform is the process known as (mechanical) twinning. Twinning results when a portion of the crystal takes up an orientation that is related to the orientation of the rest of the untwined lattice in a definite, symmetrical way. The twinned portion of the crystal is a mirror image of the parent crystal. The plane of symmetry between the two portions is called the twinning plane. Twinning differs from slip in several specific ways well described in Dieter [12].
It is known that, in general, when a steel experiences high strain rates, twinning should be a mechanism by which the metal deforms [12]. Furthermore, it is also known that increasing the strain rate by a factor of 103 greatly increases the number of observed twins [13]. Therefore, if the strain rates in cutting areas is as high as is believed, all the plastic deformation observed in cutting should be governed by twinning, and neither the slip-line theory nor other methods of the mathematical theory of plasticity are applicable to study the deformation process in cutting. However, this is not the case in metal cutting because:
(1) The maximum contribution which the twining shear could make to the observed strain is about 17% which is only a small fraction of the strain commonly observed in cutting.
(2) The multiple micrographs of the chip deformation zone presented in this book and those published in literature [16, 17] illustrate the result of typical plastic deformation by slip.
(3) Microstructure of twins [12,13], which is very different from that of slipping, has never been observed on the reported micrographs of the deformation zone and chip.
Therefore, this simple consideration shows that the calculated high strain rate in metal cutting does not conform to the available experimental data.
References:
1. Drucker, D., An analysis of the mechanics of metal
cutting, Journal of Applied Physics, 20,
1013, 1949.
2. Shaw, M. C., Metal Cutting Principles, Clarendon
Press, Oxford, 1984.
3. Freudenthal, A. M., The Inelastic Behavior of
Engineering Materials and Strictures, John
Willey & Sons, Inc, New York, 1950.
4. Chao, B. T., and Bisacre, G. H., The effect of
speed and feed on the mechanics of metal
cutting, Proceedings of The Institution of Mechanical Engineers, 165,
1, 1951.
5. Kececioglu, D., Shear strain rate in metal cutting
and its effect on shear flow stress, ASME
Journal of Engineering for Industry, 80, 158, 1958.
6. Von Turkovich, B.F., Cutting theory and chip morphology.
Chapter 2 in Handbook of High-
speed Machining Technology, Ed.by R.I.King, Chapman and Hall, New York,
1985.
7. Oxley, P. L. B., Mechanics of Machining: An Analytical
Approach to Assessing
Machinability, John Wiley & Sons, New York, 1989.
8. Palmer, W. B. and Oxley, P. L. B., Mechanics of
metal cutting, Proc. Inst. Mech. Eng., 173,
623, 1959.
9. Oxley, P. L. B., Rate of strain effect in
metal cutting, ASME Journal of Engineering for
Industry, 84, 335, 1963.
10. Stephenson, D. A. and Agapionu, J. S.,
Metal Cutting Theory and Practice, Marcel Dekker,
Inc., New York, 1997.
11. Lei, S., .Shin, Y. C., and Incropera, F., Material
constitutive modeling under high strain rates
and temperatures through orthogonal machining tests, in “Manufacturing
Science and
Engineering,” Proceedings of 1997 ASME International Mechanical Engineering
Congress
and Exposition, November 16-21, 1997, Dallas, Texas, Vol. 6-2, 91,
1997.
12. Dieter, G. E., Mechanical Metallurgy, McGraw-Hill
Publishing Company, New York, 3rd
ed., 1986.
13. Reed-Hill, R. E., Role of deformation twinning
in the plastic deformation of a polycrystalline
anisotropic metals, Deformation Twinning, AMS, 25, 1, 1964.
14. Buchar, J., Bilek, Z., and Dusek, F., Mechanical
Behavior of Metals at Extremely High
Strain Rates, Trans Tech Publications, Ltd., Switzerland, 1986.
15. Hertzberg, R. W., Deformation and Fracture
Mechanics of Engineering Materials, Wiley,
New-York, 3rd ed., 1989.
16. Zorev, N. N., Metal Cutting Mechanics, Pergamon
Press, Oxford, 1966.
17. Trent, E.M., Metal Cutting, 3nd. Ed., Butterworth-Heinemann
Ltd., Oxford, 1991.